Закон Ома для полного участка цепи: источник постоянного тока и вывод закона.
Рассмотрим источник постоянного тока, представленный сосудом с серной кислотой и внутри него – цинковым и угольным электродами. Под действием закона сохранения заряда цинк переходит в форму двухвалентных ионов, обретая отрицательный заряд. Для вывода закона Ома рассмотрим полный участок цепи, включая резистор, подключенный между электродами. Это приводит к установлению постоянного электрического тока: избыток электронов с цинкового электрода начинает движение к угольному. Химическая реакция влечет за собой работу A по передаче заряда q, которую можно выразить через ЭДС:
ε = A/q
Также с учетом закона сохранения энергии эта работа расходуется на выделение тепла Q в нагрузке и в самом источнике:
A = Q
Количество тепла, выделенное в источнике и нагрузке, определяется законом Джоуля-Ленца:
Q = I²• r • t, где r – сопротивление источника
и
Q = I²• R • t, где R – сопротивление нагрузки
Заряд q также можно выразить через силу тока I и время t:
q = I • t
Путем преобразований мы получаем выражение для ЭДС полной цепи:
ε • I • t = I²• r • t + I²• R • t
⇓
ε = I•r + I•R – из этого выражения выводится формула закона Ома для полной цепи:
I = ε/(r+R)
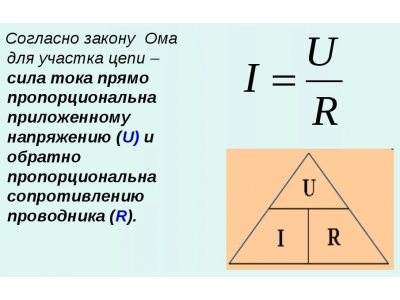
Классическая формулировка закона Ома для полной цепи: сила тока полной цепи пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи.
В большинстве случаев сопротивление источника намного ниже сопротивления нагрузки: R ≫ r. В таких ситуациях приближенно можно считать ε ≈ U, а формула принимает вид уравнения закона Ома для участка цепи:
I = U/R.
Интересно отметить, что изначально выбранные символы Георгом Омом отличаются от современных.
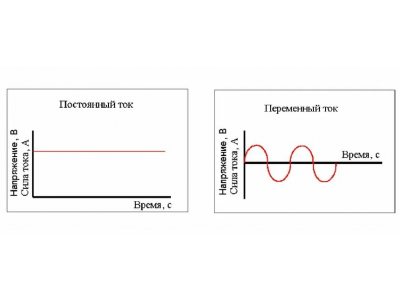
Закон Ома для переменного тока.
Рассмотрим случай токов, подчиняющихся гармоническому закону. В реальных цепях, помимо активной (резистивной) нагрузки, часто встречаются реактивные элементы: емкости и индуктивности, создавая колебательный контур. Эти элементы представляют реактивную составляющую нагрузки, усложняющую расчеты.
Рассмотрим последовательную цепь с резистором, конденсатором и катушкой в установившемся режиме, подключенную к источнику ЭДС с низким внутренним сопротивлением. Напряжение на резисторе и ток совпадают по направлению. В катушке возникает ЭДС индукции, противодействующая изменению напряжения, а в конденсаторе напряжение препятствует току. Фазы колебаний в них отличаются: в катушке напряжение опережает ток, в конденсаторе - наоборот.
За основу векторной диаграммы возьмем ток, так как он одинаков на всех элементах. В резисторе напряжение совпадает с током. В катушке - ЭДС индукции, а в конденсаторе - противодействие току.
Формула для результирующего напряжения:
U R = I ⋅ R
U L = I ⋅ X L
U C = I ⋅ X C
где X C - емкостное сопротивление, X L - индуктивное сопротивление.
Полное сопротивление, называемое импедансом и обозначаемое Z, учитывает и активное и реактивное сопротивление. При установившемся режиме:
Z = √(R² + (X L - X C)²)
С учетом всех параметров можно записать закон Ома для полной цепи переменного тока:
I = U / Z
Таким образом, закон Ома применяется не только для постоянного тока, но и для переменного тока, учитывая реактивные элементы и особенности колебательных контуров.
Рекомендуемые статьи
Шина заземления. Описание и применение
Заземление предназначенно для электрического соединения различных приборов непосредственно с землей. Эта конструкция принимает на себя отведенные токоотводом от молниеприемника удары молнии и рассеивает в грунте.Шина заземления (шина земля - ноль) – это тот элемент, который в обязательном порядке располагается в каждом электрическом щитке и соединяется с контуром действующего заземления. Иными сло..
Реле - виды, устройство, применение
Что такое реле Реле - это электромеханическое устройство, которое используется для управления электрическими сигналами и силовыми цепями.Реле используется для множества задач, например:Управление высоковольтными и высокотоковыми цепями, такими как управление электрическими двигателями, освещением и обогревом.Контроль и защита электрических цепей, таких как автоматический выключатель, предохра..
Допустимые токовые нагрузки для кабелей с медными и алюминиевыми жилами
Допустимые токовые нагрузки для кабелей с медными жилами Рассчитать сечение провода на практике довольно просто. Зная диаметр проводника, например, измерив его штангенциркулем, можно быстро вычислить площадь сечения по формуле S = 3,14х(D/2)². Если жила круглая - то площадь сечения определяется по формуле площади круга (3,14 х радиус в квадрате). Конечно, это не совсем корректная формула, но ..
Постоянный и переменный ток что это? Чем отличается Постоянный ток (DC) и Переменный ток (AC)
Процесс электрического тока можно аналогично сравнить с перемещением воды из резервуара с более высоким уровнем жидкости в резервуар с более низким уровнем. Вода течет по трубе, соединяющей резервуары, пока разница в уровнях воды сохраняется. Движение воды в трубе прекращается, когда давление на обоих концах трубы становится равным. Непрерывный поток воды достигается при наличии разницы давления, ..
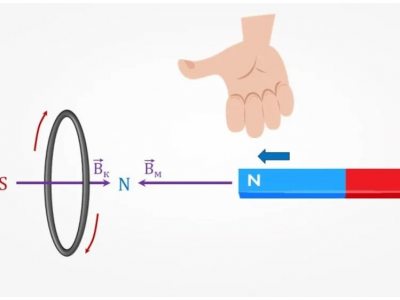
Как пользоваться правилом Ленца?
Правило Ленца является важным правилом в электромагнетизме, которое описывает направление индуцированного электрического тока в замкнутом контуре, когда изменяется магнитное поле в этом контуре. Это правило формулируется следующим образом:При изменении магнитного поля в замкнутом проводящем контуре индуцируется электрический ток, направление которого таково, что он создает магнитное поле, противоп..